A Common Mistake in Lifetime-Based FRET Measurement

Wolfgang Becker, Axel Bergmann, Becker & Hickl GmbH

Abstract: FRET efficiencies derived from FLIM FRET experiments are obtained from the ratio of the fluorescence lifetimes of the FRET donor in presence and in absence of the acceptor. It is implicitly assumed that when the FRET intensity changes the donor lifetime linearly follows the donor intensity. It is therefore expected that the FLIM-based FRET efficiency reflects the FRET efficiency obtained in intensity-based FRET experiments. We show that this is wrong. A part of the donor does not participate in the FRET, and the donor fluorescence decay profile becomes double exponential. A single-exponential approximation of the donor lifetime does not represent the donor intensity, and the FLIM-FRET efficiency no longer reflects the Intensity-FRET efficiency. Correct FRET efficiencies are only obtained by double-exponential decay analysis and using the amplitude-weighted average of the donor-component lifetimes for calculating the FRET efficiency. We further show that useful FRET efficiencies can be calculated from the lifetime of the decay component of the interacting donor. These interacting-donor FRET efficiencies are free of the influence of the non-interacting donor fraction. Interacting-donor FRET efficiencies can be converted directly into donor-acceptor distances.

FRET Efficiency

Förster resonance energy transfer (FRET) is an interaction of two fluorophore molecules (or, more exactly a fluorophore and an absorber) that are located in close distance to each other. If the emission band of one fluorophore overlaps the absorption band of the other energy from the first dye, the donor, is transferred to the second one, the acceptor [17, 18], see Fig. 1, left. Because of its dependence on the donor-acceptor distance FRET measurements have become an important tool of cell biology [22, 23, 24, 25]. The efficiency of the energy transfer, or the 'FRET efficiency', has originally been defined as

              (1)

where I_DA is the donor intensity in presence of an acceptor, I_D the donor intensity in absence of an acceptor.

Intensity-based FRET measurements are difficult because intensities depend on the concentration of the fluorophore, the excitation power, and the sensitivity of the detection system. Therefore calibration measurements from cells containing only the donor and the acceptor are required [19]. These make the technique difficult to use and susceptible to systematic errors.

Calibration problems can be avoided by lifetime-based FRET measurement [1, 2]. When FRET occurs the donor is loosing part of its energy to the acceptor, with the effect that its fluorescence lifetime becomes shorter, see Fig. 1, right.

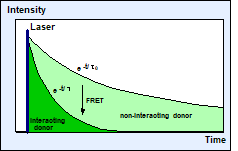
Fig. 1: Förster-resonance energy transfer. The lifetime of the donor becomes shorter when it interacts with an acceptor.

The lifetime-based FRET efficiency is:

             (2)

t_DA is the donor lifetime in presence of acceptor, t_D is the donor lifetime in absence of acceptor.

The lifetime-based FRET efficiency (2) can be derived from the intensity-based one under the presumption that the donor intensity and the donor lifetime are proportional to each other.

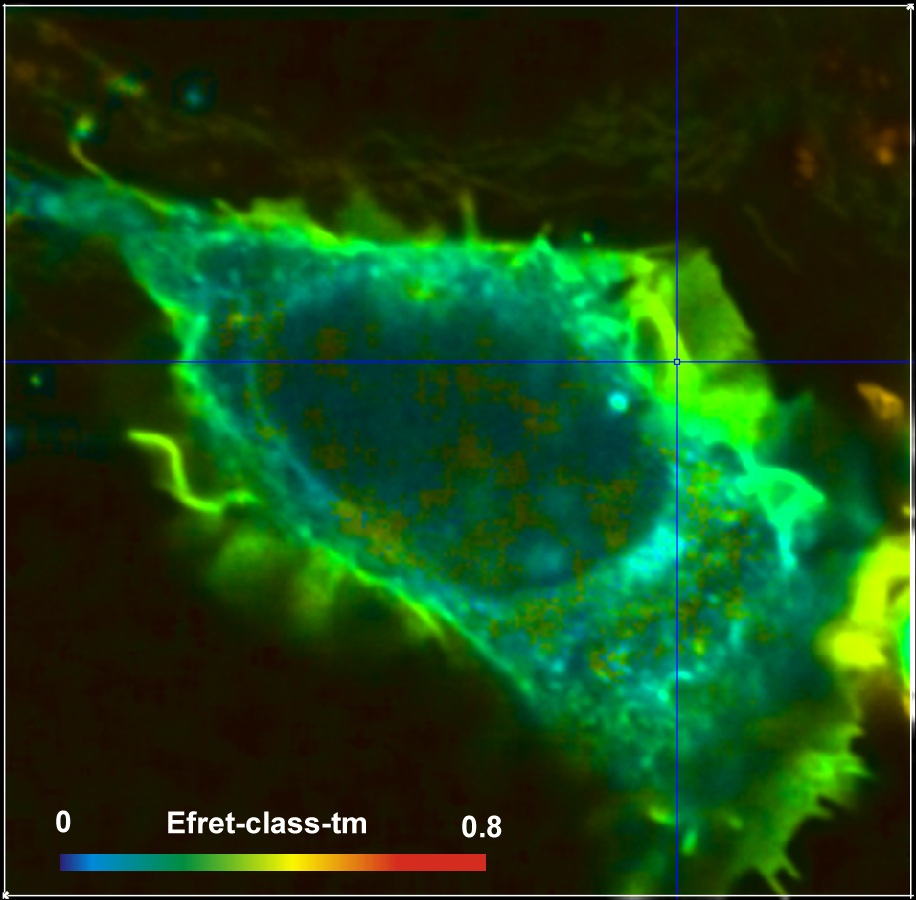
An example for a FRET measurement is shown in Fig. 2. The cell expresses two interacting proteins, one linked to the donor, CFP, the other to the acceptor, YFP. FRET occurs in locations where the proteins interact. A lifetime image is shown on the left, an image of the FRET efficiency on the right.

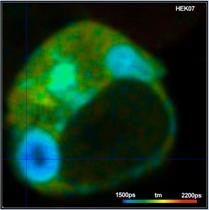
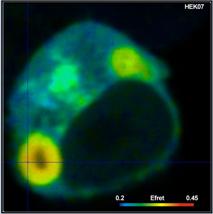
Fig. 2: HEK cell expressing two interacting proteins, one labelled with the donor, CFP, the other with the acceptor, YFP. Donor image. Left: Lifetime image. Right: Image of the FRET efficiency.

The FLIM-FRET technique outlined above is easy to use and robust. It has been used for many years and for a wide variety of protein interaction studies, see for example [13, 14, 15, 16, 25]. For an overview on the FLIM FRET literature please see [1].

Despite the amazing success of FLIM FRET the technique has a hidden problem: The definition of the FLIM FRET efficiency implicitly assumes that the donor decay is single-exponential. In real FRET system this is not the case, see decay curves in Fig. 3.

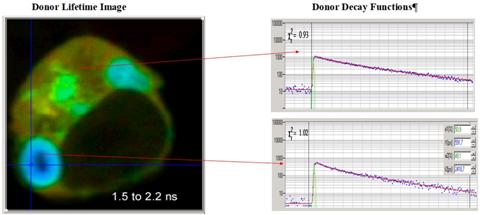
Fig. 3: HEK cell, expressing two interacting proteins, labelled with CFP (donor) and YFP (acceptor). Note the multi-exponential profile of the decay curves.

The multi-exponential decay of the FRET donor has been ignored for many years. Now, there is little doubt that it comes from the presence of a non-interacting donor fraction. The resulting donor decay functions can be approximated by a double-exponential model, with a fast component from the interacting donor fraction and a slow lifetime component from the non-interacting donor fraction [1, 2, 11, 12]. The double-exponential nature of the interacting-donor decay has consequences to the definition of the FRET efficiency.

FLIM FRET Efficiency from Double-Exponential Donor Decay

A double-exponential decay is described by two lifetimes, t₁ and t₂, and two amplitude coefficients, a₁ and a₂:

f(t) = a₁ e^-t/t1 + a₂ e^-t/t2

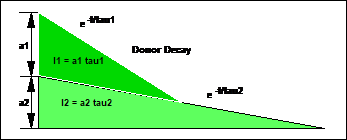
Fig. 4: Amplitudes and intensities of the components of a double-exponential decay

However, the definition of the FLIM-FRET efficiency uses only one lifetime, t_DA, to describe the decay time of the interacting donor. So, what is the 'Lifetime' of a double-exponential decay?

The problem is normally solved by using a single-exponential approximation of the double-exponential decay. In other words, t_DA  is replaced with a weighted average of the component lifetimes, t₁ and t₂. There are two different definitions for this average. The most common one is the 'Intensity-Weighted Lifetime', or t_i. It weighs the lifetimes of the decay components by their intensities, i.e. the areas under the components. These are a₁t₁ for the fast component and a₂t₂ for the slow component.

The second definition weighs the component lifetimes by their amplitudes, a₁ and a₂. The result is the 'Amplitude-Weighted Lifetime'. It is usually called 'Mean Lifetime', t_m. The mathematical expressions of t_i and t_m are:

         Intensity-Weighted Lifetime      Amplitude-Weighted Lifetime

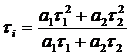
                               with       

Which lifetime is the correct one to calculate the FRET efficiency? The definition of the FLIM-based FRET efficiency leaves it open. The answer can be found by taking a close look at the equations above.

The definition of the FLIM-FRET intensity (2) derives from the definition of the intensity-FRET intensity (1). Therefore, the terms in the definitions of t_i  and t_i should be in some reasonable relationship with the intensity of the donor. There is no such relationship for the products a₁t₁² and a₂t₂² in the definition of t_i . Therefore, using t_i for t_DA in (2) does not make sense. Its use for calculating the FRET efficiency leads to wrong results.

The situation is different for t_m. The products a₁t₁ and a₂t₂ in the definition of t_m are the areas under the decay components, i.e. intensities. The sum of both represents the intensity of the donor. Therefore, t_m has to be used for t_DA to obtain an equivalent of the intensity-based FRET efficiency (1). That means the FLIM FRET efficiency is

The fact that the amplitude-weighted lifetime must be used to calculate E_fret has implications on FLIM systems for FRET measurements in general. t_m is only obtained by recording well resolved decay functions and splitting them into exponential components by double-exponential decay analysis. A FLIM system or a FLIM technique which does not build up detailed decay functions in the individual pixels is not able to deliver t_m. This is especially the case for many 'Fast FLIM' techniques which produce only 'Lifetimes' instead of decay functions [21]. These lifetimes are equivalent to the intensity-weighted lifetime and are thus not suitable to determine FRET efficiencies. The same is the case for a number of 'Rapid Lifetime Analysis' techniques. These are usually based on ratios of gated intensities or moments of the measured decay signals. Also these lifetimes are intensity-weighted and unsuitable for the measurement of FRET efficiencies.

That the FRET efficiency has to be calculated from the amplitude-weighted lifetime has already been pointed out by J.R.L. Lakowicz in his 1999 edition of 'Principles of Fluorescence Spectroscopy'. Until now, this has not been commonly noticed, although the book and its 2006 successor [20] is constantly cited in fluorescence papers.

Double-Exponential Decay Analysis

As explained above, correct determination of the FRET efficiency requires double-exponential decay analysis. Multi-exponential analysis of FLIM data is often considered difficult of even impossible. However, the efficiency of decay analysis depends dramatically on the composition of the decay profiles. For typical donor decay data with t_DA/ t_D ratios larger than four the options are not as bad as commonly believed. Moreover, in the last decade, the capabilities of multi-exponential FLIM recording and data analysis have increased considerably. More sensitive detectors have increased the number of photons in the FLIM data [9], the time resolution of detectors and TCSPC systems has increased [6, 7, 8], Maximum-Likelihood Estimation (MLE) and intelligent binning have reduced the number of photons per pixel needed for double-exponential FLIM analysis [3], and GPU processing has reduced the data processing time [3]. With these improvements, FLIM data analysis is not only able to deliver the amplitude-weighted lifetime, t_m, but also the lifetimes, t₁ and t₂, and the amplitudes, a₁ and a₂, of the two decay components. The meaning of these parameters is illustrated in Fig. 5.

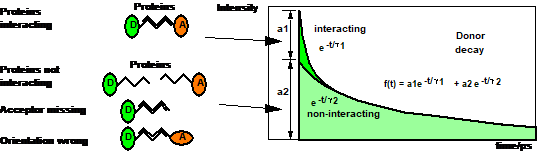
Fig. 5: Donor fluorescence decay components in a FRET system

The availability of these parameters makes it possible to calculate the FLIM FRET Efficiency:

                            E_fret = 1- t_m/t_D    or  E_fret = 1- (a₁t₁ + a₂ t₂) / t_D

Moreover, the slow decay component of the donor decay, t₂, is identical with the donor lifetime in absence of the acceptor, t_D. E_fret then becomes

                            E_fret = 1- t_m/t₂    or  E_fret = 1- (a₁t₁ + a₂ t₂) / t₂

This equation contains only parameters that are determined by analysis of the measured donor decay. That means double-exponential FRET analysis works without external calibration [5].

Interacting-Donor FRET Efficiency

Another frequent mistake in FRET calculations is to use the classic intensity FRET or FLIM FRET efficiency to calculate donor-acceptor distances. It has been shown above that the donor decay function is the sum of a decay component from interacting donor and a decay component from non-interacting donor. Even if the correct lifetime, t_m, is used E_fret does not represent the real FRET efficiency of the interacting-donor fraction. Also this problem can be solved by double-exponential FRET analysis.

The pure interacting-donor FRET efficiency is obtained by using the lifetime, t₁, of the interacting donor fraction in the equation of the FRET efficiency:

     E_interact = 1- t₁ /t_D 

Again, t_D is identical with the lifetime of the non-interacting donor, t₂, i.e.:

     E_interact = 1- t₁ /t₂ 

E_interact can be directly converted into the donor-acceptor distance, r, relative to the Förster radius, r₀:

     ( r / r₀ ) = 1 / E_interact - 1     or, more directly:    ( r / r₀ ) = t₁ / (t₂ - t₁₎,     with r₀ = Förster radius

FRET analysis based on these considerations is described in [3, 4, 5].

Comparison of Different Definitions of the FRET efficiency

FRET efficiencies based on different definitions for two different cells are compared in Fig. 6. Left to right, the images show the FRET efficiency calculated from the intensity-weighted lifetime, t_i, the amplitude-weighted lifetime, t_m, and from the interacting-donor lifetime, t₁. Colour scaling is the same for all images. Average FRET efficiencies are shown above the images.

E_fret-ti = 0.18                                         E_fret-tm = 0.35                                                E_interact = 0.72

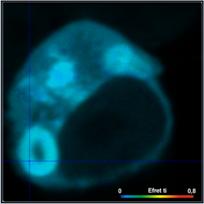
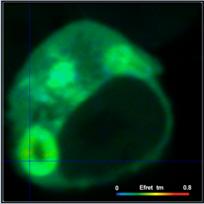
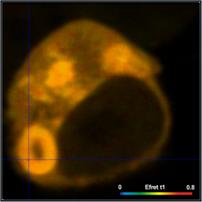
E_fret-ti = 0.24                                                 E_fret-tm = 0.4                                            E_interact = 0.65

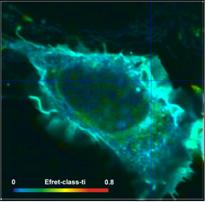
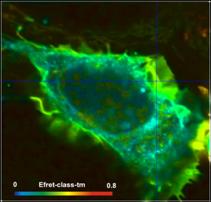
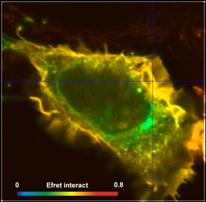
Fig. 6: FRET efficiencies based on different definitions are compared for two different cells. Left to right: FRET efficiency calculated from the intensity-weighted lifetime, ti, the amplitude-weighted lifetime, tm, and from the interacting-donor lifetime, tfret.

All images were calculated by bh SPCImage NG FLIM analysis software. Maximum-Likelihood Estimation (MLE) in combination with a double-exponential incomplete-decay model was used to fit the donor decay data. The images of the FRET efficiencies were calculated by SPCImage parameter calculation functions [3].

As can be seen from Fig. 6, the differences between the different FRET efficiency definitions are substantial. The difference between the t_i and the t_m efficiencies are almost 1:2. This is hardly tolerable for characterising protein interaction in cells. FRET efficiencies calculated from intensity-weighted lifetimes or from single-exponential approximations should therefore not be used in FRET experiments.

Of course, there are also differences between the t_m-based efficiencies and the t₁-based efficiencies (E_interact). However, this is not surprising. The differences are explained by the fact that a substantial fraction of the donor molecules does not participate in the FRET and, consequently, biases the t_m FRET efficiency towards lower values. Whether the t_m efficiency or the t_fret efficiency is to be used depends on the application. t_m-based efficiencies should be used for comparing FLIM FRET results with intensity-FRET results, t_fret-based efficiencies (E_interact) for comparing donor-acceptor distances.

FRET Analysis by SPCImage NG

It is unlikely that you will obtain or have obtained wrong FRET efficiencies with bh FLIM systems and bh SPCImage data analysis. From the earliest versions on, the default lifetime for multi-exponential decay was the amplitude-weighted lifetime t_m. We did this as a courtesy to FRET users. Moreover, the SPCImage data calculation and data display functions contain the t_m‑based classic FRET efficiency, E_class, and the interacting-donor FRET efficiency, E_int. Both are calculated correctly. The only mistake you can possibly do is to run a single-exponential fit or a first-moment analysis on the FLIM-FRET data. However, in this case SPCImage would deliver improbable E_class and E_int values so that the mistake would be noticed.

Summary

FRET efficiencies derived from FLIM FRET experiments are traditionally obtained from the ratio of the fluorescence lifetimes of the FRET donor in presence of the acceptor and in absence of the acceptor. The definition is derived from the intensity-based definition of the FRET intensity, which uses the ratio of the corresponding intensities. It is implicitly assumed that the donor lifetime in presence of the acceptor linearly follows the (normalised) intensity. It is therefore expected that the FLIM-based FRET efficiency reflects the intensity-based FRET efficiency. These assumptions are correct when the donor decay is single-exponential. This is, however, not the case. One part of the donor fluorescence comes from non-interacting donor molecules, another part from interacting ones. The resulting fluorescence decay is double-exponential. The classic definition does not take this into account.  It contains only one lifetime for the 'donor in presence of an acceptor'. The problem is usually solved by using an average - or 'apparent' - lifetime of the donor decay. The usual approach is to use an intensity-weighted average, t_i, of the lifetimes of the two components. The intensity-weighted average is used because t_i is identical with the lifetime of a single-exponential approximation or the 'apparent' lifetime of the donor decay.

Unfortunately, the intensity-weighted lifetime does not linearly represent the donor intensity, and the FLIM-FRET efficiency based on it is not identical with the Intensity-FRET efficiency. To obtain correct FLIM-FRET efficiencies, the amplitude-weighted average of the donor component lifetimes, t_m, must be used. The amplitude weighted lifetime can only be obtained by recording well resolved donor decay functions, analysing them with a double-exponential decay model, and calculating the amplitude-weighted lifetime from the decay parameters.

A third FLIM-FRET efficiency can be obtained by using of the decay component of the interacting donor for t_DA. The resulting FRET efficiency is, of course, different from the intensity-based FRET efficiency. However, it represents the FRET efficiency exclusively for the interacting donor molecules, without the influence of the non-interacting donor fraction. The interacting-donor FRET efficiency is therefore higher than the Intensity-FRET or the FLIM-FRET efficiency. Its advantage is that it can be converted directly into donor-acceptor distances.

References

1.            W. Becker, The bh TCSPC Handbook. 9th ed. Becker & Hickl GmbH (2021)

2.            W. Becker, Advanced time-correlated single-photon counting techniques. Springer, Berlin, Heidelberg, New York, 2005

3.            SPCImage Data Analysis, in W. Becker, The bh TCSPC Handbook. 9th ed. Becker & Hickl GmbH (2021)

4.            W. Becker, Molecular imaging by TCSPC FLIM - Application to metabolic imaging and FRET imaging. One-day symposium on advanced microscopy techniques in the biomedical sciences, Charlottesville, 2023

5.            W. Becker, Axel Bergmann, Double-exponential FLIM-FRET is free of calibration. Application note, www.becker-hickl.com (2023)

6.            W. Becker, C. Junghans, V. Shcheslavskiy, High-Resolution Multiphoton FLIM Reveals Ultra-Fast Fluorescence Decay in Human Hair. Application note, www.becker-hickl.com (2023)

7.            W. Becker, A. Bergmann, C. Junghans, Ultra-Fast Fluorescence Decay in Natural Carotenoids. Application note, www. becker-hickl.com (2022)

8.            Becker & Hickl GmbH, Sub-20ps IRF Width from Hybrid Detectors and MCP-PMTs. Application note, www.becker-hickl.com (2017)

9.            W. Becker, B. Su, K. Weisshart, O. Holub, FLIM and FCS Detection in Laser-Scanning Microscopes: Increased efficiency by GaAsP Hybrid Detectors. Micr. Res. Tech. 74, 804-811 (2011)

10.         W. Becker, The bh TCSPC Handbook. 1st ed. Becker & Hickl GmbH (2005)

11.         W. Becker, A. Bergmann, M.A. Hink, K. König, K. Benndorf, C. Biskup, Fluorescence lifetime imaging by time-correlated single photon counting, Micr. Res. Techn. 63, 58-66 (2004)

12.         W. Becker, K. Benndorf, A. Bergmann, C. Biskup, K. König, U. Tirlapur, T. Zimmer, FRET measurements by TCSPC laser scanning microscopy, Proc. SPIE 4431, 94-98 (2001)

13.         B. J. Bacskai, J. Skoch, G.A. Hickey, R. Allen, B.T. Hyman, Fluorescence resonance energy transfer determinations using multiphoton fluorescence lifetime imaging microscopy to characterize amyloid-beta plaques, J. Biomed. Opt 8, 368-375 (2003)

14.         R. Cao, H. Wallrabe, K. Siller, S. R. Alam, A. Periasamy, Single cell redox states analyzed by fluorescence lifetime metrics and tryptophan FRET interaction with NAD(P)H. Cytometry Part A, 96A, 110-121 (2019)

15.         Y. Chen, A. Periasamy, Characterization of two-photon excitation fluorescence lifetime imaging microscopy for protein localization, Microsc. Res. Tech. 63, 72-80 (2004)

16.         R.R. Duncan, A. Bergmann, M.A. Cousin, D.K. Apps, M.J. Shipston, Multi-dimensional time-correlated single-photon counting (TCSPC) fluorescence lifetime imaging microscopy (FLIM) to detect FRET in cells, J. Microsc. 215, 1-12 (2004)

17.         Th. Förster, Zwischenmolekulare Energiewanderung und Fluoreszenz, Ann. Phys. (Serie 6) 2, 55-75 (1948)

18.         Th. Förster, Energy migration and fluorescence. Translated by Klaus Suhling. J. Biomed. Opt. 17 011002-1 to -10 (2012)

19.         G.W. Gordon, G. Berry, X.H. Liang, B. Levine, B. Herman, Quantitative Fluorescence Resonance Energy Transfer Measurements Using Fluorescence Microscopy. Biophys. J. 74, 2702-2713 (1998)

20.         J.R. Lakowicz, Principles of Fluorescence Spectroscopy, 3rd edn., Springer (2006)

21.         X. Liu, D. Lin, W. Becker, J. Niu, B. Yu, L. Liu, J. Qu, Fast fluorescence lifetime imaging techniques: A review on challenge and development. Journal of Innovative Optical Health Sciences, 1930003-1 to -27 (2019)

22.         A. Periasamy, Methods in Cellular Imaging. Oxford University Press, Oxford New York (2001)

23.         A. Periasamy, R.M. Clegg, eds., FLIM Microscopy in Biology and Medicine. CRC Press 2009

24.         A. Periasamy, N. Mazumder, Y. Sun, K. G. Christopher, R. N. Day, FRET Microscopy: Basics, Issues and Advantages of FLIM-FRET Imaging. In: W. Becker (ed.) Advanced time-correlated single photon counting applications. Springer, Berlin, Heidelberg, New York (2015)

25.         Y. Sun, C. Rombola, V. Jyothikumar, A. Periasamy,  Förster resonance energy transfer microscopy and spectroscopy to localize protein-protein interactions in live cells. Cytometry A, 83A(9), 780-793 (2013)

Contact:

Wolfgang Becker

Becker & Hickl GmbH

Berlin, Germany

Email: becker@becker-hickl.com