Double-Exponential FLIM-FRET Approach is Free of Calibration

Wolfgang Becker, Axel Bergmann, Becker & Hickl GmbH

Abstract: A new double-exponential FLIM-FRET approach obtains FRET parameters from a single lifetime image of the donor. The technique makes use of the fact that the donor decay functions contain a component from non-interacting donor. Becker & Hickl SPCImage NG data analysis software determines the lifetimes and the amplitudes of the decay components. From these, SPCImage calculates the classic FRET efficiency, the FRET efficiency of the interacting donor, the amount of interacting donor, and the ratio of the donor-acceptor distance to the Förster radius. By using the lifetime of the non-interacting donor fraction as a reference lifetime the method avoids the need for reference data from separate donor-only cells. This not only makes the technique easy to use but also prevents differences in the metabolic state or in the molecular environment from influencing the FRET results. At the end of this application note we present a protocol for double-exponential FRET analysis with bh SPCImage NG.

Förster Resonance Energy Transfer (FRET)

Förster resonance energy transfer (FRET) is an interaction of two fluorophore molecules (or, more exactly a fluorophore and an absorber) that are located in close distance to each other. If the emission band of one dye - the donor - overlaps the absorption band of the other - the acceptor - energy from the donor is transferred to the acceptor. The principle is shown schematically in Fig. 1.

Fig. 1: Principle of FRET. Light is absorbed by one molecule, the donor, and transferred to a second molecule, the acceptor. The energy absorbed by the donor is finally emitted by the acceptor.

The efficiency of this process is the 'FRET efficiency', defined as

              (1)

where I_DA is the donor intensity in presence of an acceptor and I_D the donor intensity in absence of an acceptor.

The theory of the effect was developed by Theodor Förster and published in 1948 [18, 19]. The energy transfer rate from the donor to the acceptor decreases with the sixth power of the distance. Therefore it is noticeable only at distances shorter than 10 nm [21 Lakowicz Principles 1999]. Because of its dependence on the distance FRET has become an important tool of cell biology [22, 23, 24, 25]. Different proteins are labelled with a donor and an acceptor and the FRET efficiency is measured. The FRET efficiency is then used to proof protein interaction or to determine donor-acceptor distances on the nm scale. Donor and acceptor can also be linked to the same protein. The FRET efficiency is then an indicator of protein folding and protein conformation.

Intensity-FRET measurements have a number of problems. Intensities depend on the concentration of the fluorophore and on the excitation power. The reference intensity, I_D, cannot be obtained under identical conditions as I_DA. Calibration measurements from different cells are required [20], which makes the technique difficult to use and susceptible to systematic errors.

Lifetime-Based FRET

These problems are avoided by lifetime-based FRET measurement [1, 2, 12, 13]. When FRET occurs the donor is loosing part of its energy to the acceptor, with the effect that its fluorescence lifetime becomes shorter, see Fig. 2, right.

Fig. 2: Förster-resonance energy transfer. The lifetime of the donor becomes shorter when it interacts with an acceptor.

The lifetime-based FRET efficiency is:

             (2)

t_DA is the donor lifetime in presence of acceptor, t_D is the donor lifetime in absence of acceptor.

The lifetime-based FRET efficiency (2) is equivalent to the intensity-based one under the presumption that the lifetimes, t_DA and  t_D , are proportional to the relative intensities I_DA and I_D [5].

The use of FLIM FRET has the obvious advantage that the FRET intensity is obtained from a single lifetime image of the donor in the FRET system in combination with a reference lifetime image of the donor in absence of an acceptor. The FLIM-FRET technique outlined above is easy to use and robust. It has been used for a wide variety of protein interaction studies, see for example [14, 15, 15, 17, 25]. For an overview on the FLIM FRET literature please see [1].

An example is shown in Fig. 3. The cell expresses two interacting proteins, one linked to the donor, CFP, the other to the acceptor, YFP. FRET occurs in locations where the proteins interact. A lifetime image is shown on the left, an image of the FRET efficiency on the right.

Fig. 3: HEK cell expressing two interacting proteins, one labelled with the donor, CFP, the other with the acceptor, YFP. Donor image. Left: Lifetime image. Right: Image of the FRET efficiency.

Fig. 4 shows how the FRET efficiency varies throughout the cell and, consequently, where in the cell the proteins interact. The FLIM-FRET approach is therefore commonly used for protein interaction and protein conformation experiments. However, a close inspection of the decay functions turns up a possible problem: The decay curves are not single-exponential. The deviation from single-exponential behaviour is the larger the higher the FRET efficiency is, see Fig. 4.

Fig. 4: HEK cell, expressing two interacting proteins, labelled with CFP (donor) and YFP (acceptor).

The multi-exponential profile of the donor decay raises questions on the interpretation of FLIM FRET data in general and on the applicability of the definition of the FRET efficiency. In particular, it requires clarification of which lifetime should be used in the definition of the lifetime-based FRET efficiency [5].

Double-Exponential Donor Decay

The multi-exponential decay of the FRET donor has been ignored for many years. Now, there is little doubt that it comes from the presence of a non-interacting and an interacting donor fraction. The resulting donor decay functions can be approximated by a double exponential model, with a fast component from the interacting donor molecules and a slow lifetime component from the non-interacting donor molecules [1, 2, 13]. There are several reasons why a donor may not interact. Its protein may just not be linked to an acceptor protein, the acceptor protein may not be labelled with the acceptor, or the orientation between the donor and the acceptor may be wrong. These situations are illustrated in Fig. 5, left. Whatever the reasons of missing donor-acceptor interaction are, the result is a double-exponential decay curve, shown schematically in Fig. 5, right.

Fig. 5: Components of the donor decay in FRET systems

FRET Parameters from Double-Exponential Decay Analysis

In the last decade, the capabilities of multi-exponential FLIM recording and data analysis have increased considerably. More sensitive detectors have increased the number of photons in the FLIM data [10], the time resolution of detectors and TCSPC systems has increased [7, 8, 9], Maximum-Likelihood Estimation (MLE) and intelligent binning have reduced the number of photons per pixel needed for double-exponential FLIM analysis [3], and GPU processing has reduced the data processing time [3].

With these improvements, FLIM data analysis is able to deliver the lifetimes, t₁ and t₂, and the amplitudes, a₁ and a₂, of the two decay components. t₁ is the lifetime of the interacting donor fraction, t₂ the lifetime of the non-interacting donor fraction. The lifetime of the non-interacting donor fraction,t₂, is identical with t_D in the definition of the FLIM-FRET Efficiency. t_D can therefore be replaced with t₂. By eliminating t_D the classic FRET efficiency E_fret, the true FRET efficiency of the interacting donor, E_interact [1, 2, 15], the ratio of the donor-acceptor distance and the Förster radius, r/r₀ , and the ratio of the number of interacting and non-interacting donor molecules, N_fret / N₀ can be calculated exclusively from the decay parameters delivered by double-exponential decay analysis of the donor decay:

     E_fret = 1- t_m /t₂ ,    with t_{m =} a₁t_{1 +} a₂t₂, amplitude-weighted lifetime of double-exponential decay

     E_interact = 1- t₁ /t₂ 

     ( r / r₀ ) = 1 / E_interact - 1     or    ( r / r₀ ) = t₁ / (t₂ - t₁),     with r₀ = Förster radius

     N_fret / N₀ = a₁ / a₂             

The double-exponential FRET approach has been introduced by bh already in 2004 and 2005 [2, 11, 12] but attracted little attention. Nevertheless, it has significant advantages over the classic one.

The first one is that it does not need external reference data from a donor-only cell. The reference lifetime is the lifetime, t₂, of the non-interacting donor fraction. It is obtained from the same measurement, the same cell, the same pixels, and the same environmental conditions as the interacting-donor lifetime, t₁. The double-exponential FRET approach is therefore more robust than the classic one [4]. Moreover, the double-exponential approach is much easier to use than the traditional one. Just record a FLIM data set of the sample at the donor emission wavelength, let the FLIM analysis fit the decay data and let it calculate the FRET parameters you are interested in.

Second, the method delivers correct classic FRET efficiencies. In contrast to the liftime from a single-exponential fit, the mean lifetime,t_{m =} a₁t_{1 +} a₂t₂, directly follows the donor intensity so that the FLIM-FRET efficiency reproduces the Intensity-FRET efficiency [5].

Third, it delivers the real FRET efficiency, E_interact, of the interacting donor. Donor-acceptor distances calculated from this efficiency are independent of the ratio of the amounts on interacting and non-interacting donor. This is not the case for the classic FRET efficiency: By using an average of the donor decay components it mingles the effects of the donor-acceptor distance and the interacting / non-interacting donor ratio.

The fourth advantage is that the method delivers the relative amount of interacting donor. This is real biological information which cannot be obtained from Intensity-FRET of classic FLIM FRET approaches.

An example is shown in Fig. 6. FLIM-FRET data were recorded by a bh SPC-150 TCSPC FLIM module with a HPM-100-40 hybrid detector on a Zeiss LSM 880. A single fluorescence-lifetime image was taken at the emission wavelength of the donor. The data were analysed by bh SPCImage NG FLIM data analysis software [3]. The FLIM data were processed using a double-exponential incomplete-decay model and Maximum Likelihood Estimation (MLE). Colour coding of the classic FRET efficiency, E_fret, the FRET efficiency of the interacting donor, E_interact, the donor-acceptor distance, d/R₀, and the relative amount of interacting donor was selected to obtain images of the corresponding FRET parameters.

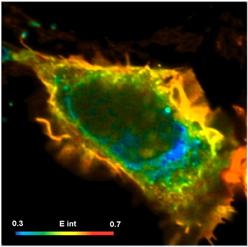
Fig. 6: HEK cell expressing two proteins labelled with Cerulean (donor) and Venus (acceptor). Interaction occurs preferentially in the cell membrane. Upper left to lower right: Classic FRET efficiency, E_fret, (E_class in SPCImage), FRET efficiency of interacting donor, E_interact, donor-acceptor distance, d/R0, relative amount of interacting donor. bh SPC-150 TCSPC FLIM module with HPM-100-40 hybrid detector, bh SPCImage NG FLIM data analysis software running on NVIDIA GPU.

Summary

Double-exponential FLIM FRET obtains FRET data from a single lifetime image of the donor. Reference data from other cells are not needed. The technique uses the fact that the donor decay function contains decay components from both non-interacting and interacting donor molecules. The lifetime of the non-interacting donor is identical with the donor lifetime in absence of an acceptor. It can thus be used as a reference lifetime for the FRET calculation. Because no external reference measurement is needed errors by possible difference in the molecular environment or in the metabolic state of the FRET cells and the reference cells are avoided. The technique is therefore more robust than the classic approach. It is also easy to use because frequent swapping of FRET samples and reference samples is avoided.

Double-exponential FLIM FRET analysis is implemented in bh's SPCImage NG data analysis software [3]. SPCImage NG fits the decay data in the pixels of the image with a double-exponential model. Using the slow decay component as a reference lifetime, it calculates the classic FRET efficiency, the FRET efficiency of the interacting donor, the amount of interacting donor, and the ratio of the donor-acceptor distance to the Förster radius. The data are presented as colour-coded images of the corresponding FRET parameters. Please see Appendix of this application note.

References

1.            W. Becker, The bh TCSPC Handbook. 9th ed. Becker & Hickl GmbH (2021)

2.            W. Becker, Advanced time-correlated single-photon counting techniques. Springer, Berlin, Heidelberg, New York, 2005

3.            SPCImage Data Analysis, in W. Becker, The bh TCSPC Handbook. 9th ed. Becker & Hickl GmbH (2021)

4.            W. Becker, Molecular imaging by TCSPC FLIM - Application to metabolic imaging and FRET imaging. One-day symposium on advanced microscopy techniques in the biomedical sciences, Charlottesville, 2023

5.            W. Becker, A Common Mistake in Lifetime-Based FRET Measurements. Application note, Becker & Hickl GmbH (2023)

6.            W. Becker, Bigger and Better Photons: The Road to Great FLIM Results. Education brochure, available on www.becker-hickl.com.

7.            W. Becker, C. Junghans, V. Shcheslavskiy, High-Resolution Multiphoton FLIM Reveals Ultra-Fast Fluorescence Decay in Human Hair. Application note, www.becker-hickl.com (2023)

8.            W. Becker, A. Bergmann, C. Junghans, Ultra-Fast Fluorescence Decay in Natural Carotenoids. Application note, www. becker-hickl.com (2022)

9.            Becker & Hickl GmbH, Sub-20ps IRF Width from Hybrid Detectors and MCP-PMTs. Application note, www.becker-hickl.com (2017)

10.         W. Becker, B. Su, K. Weisshart, O. Holub, FLIM and FCS Detection in Laser-Scanning Microscopes: Increased efficiency by GaAsP Hybrid Detectors. Micr. Res. Tech. 74, 804-811 (2011)

11.         W. Becker, The bh TCSPC Handbook. 1st ed. Becker & Hickl GmbH (2005)

12.         W. Becker, A. Bergmann, M.A. Hink, K. König, K. Benndorf, C. Biskup, Fluorescence lifetime imaging by time-correlated single photon counting, Micr. Res. Techn. 63, 58-66 (2004)

13.         W. Becker, K. Benndorf, A. Bergmann, C. Biskup, K. König, U. Tirlapur, T. Zimmer, FRET measurements by TCSPC laser scanning microscopy, Proc. SPIE 4431, 94-98 (2001)

14.         B. J. Bacskai, J. Skoch, G.A. Hickey, R. Allen, B.T. Hyman, Fluorescence resonance energy transfer determinations using multiphoton fluorescence lifetime imaging microscopy to characterize amyloid-beta plaques, J. Biomed. Opt 8, 368-375 (2003)

15.         R. Cao, H. Wallrabe, K. Siller, S. R. Alam, A. Periasamy, Single cell redox states analyzed by fluorescence lifetime metrics and tryptophan FRET interaction with NAD(P)H. Cytometry Part A, 96A, 110-121 (2019)

16.         Y. Chen, A. Periasamy, Characterization of two-photon excitation fluorescence lifetime imaging microscopy for protein localization, Microsc. Res. Tech. 63, 72-80 (2004)

17.         R.R. Duncan, A. Bergmann, M.A. Cousin, D.K. Apps, M.J. Shipston, Multi-dimensional time-correlated single-photon counting (TCSPC) fluorescence lifetime imaging microscopy (FLIM) to detect FRET in cells, J. Microsc. 215, 1-12 (2004)

18.         Th. Förster, Zwischenmolekulare Energiewanderung und Fluoreszenz, Ann. Phys. (Serie 6) 2, 55-75 (1948)

19.         Th. Förster, Energy migration and fluorescence. Translated by Klaus Suhling. J. Biomed. Opt. 17 011002-1 to -10 (2012)

20.         G.W. Gordon, G. Berry, X.H. Liang, B. Levine, B. Herman, Quantitative Fluorescence Resonance Energy Transfer Measurements Using Fluorescence Microscopy. Biophys. J. 74, 2702-2713 (1998)

21.         J.R. Lakowicz, Principles of Fluorescence Spectroscopy, 3rd edn., Springer (2006)

22.         A. Periasamy, Methods in Cellular Imaging. Oxford University Press, Oxford New York (2001)

23.         A. Periasamy, R.M. Clegg, eds., FLIM Microscopy in Biology and Medicine. CRC Press 2009

24.         A. Periasamy, N. Mazumder, Y. Sun, K. G. Christopher, R. N. Day, FRET Microscopy: Basics, Issues and Advantages of FLIM-FRET Imaging. In: W. Becker (ed.) Advanced time-correlated single photon counting applications. Springer, Berlin, Heidelberg, New York (2015)

25.         Y. Sun, C. Rombola, V. Jyothikumar, A. Periasamy,  Förster resonance energy transfer microscopy and spectroscopy to localize protein-protein interactions in live cells. Cytometry A, 83A(9), 780-793 (2013)

Appendix: Double-Exponential FLIM-FRET Protocol

Record a FLIM image of the sample at the donor emission wavelength. Use a filter that blocks emission from the acceptor. For the FLIM data format, we recommend 512x512 pixels, 1024 time channels. Use an appropriate Zoom factor so that the cell of interest reasonably fills the image area. Keep the count rate below 10⁶ photons per second. Higher count rates can be recorded by the FLIM system but the cells are unlikely to survive them. Record until you have at least 500 photons in the brightest pixel. You can see this in the Display Parameters. When ready, stop the measurement and save the data.

Transfer the data to SPCImage NG. Wait until SPCImage opens and the data appear.

Upper right in the main panel of SPCImage, select a double-exponential model. Under Options, Model, select the incomplete decay option, specify the correct pulse repetition rate, and select the MLE fit [3].

If you don't have a correct IRF from earlier measurements let SPCImage create one from the recorded data or let it optimise an existing one [3].

Select an appropriate spatial binning factor [3, 6]. For a single cell recorded with 512 x 512 pixels we recommend a binning factor of 2 or 3.

Start the fit procedure by 'Calculate Decay Matrix'. Recommendation: Have a GPU installed in the computer. Processing time without a GPU can be several minutes, with a GPU it is a few seconds [3].

The image displayed after the fit procedure is a t_m image. Click on the automatic scaling button under the parameter histogram to scale into an appropriate parameter range. If necessary, fine-tune the parameter range by shifting the cursors in the histogram panel or by typing a parameter range into the Colour parameters.

Click into Options, Colour, Coding, and select the FRET parameter you are interested in. Available are the classic FLIM FRET efficiency, E_class, the FRET efficiency of the interacting donor, E_int, the relative amount of interacting donor, a₁, the ratio of interacting and non-interacting donor, a₁/a₂, and the ratio of the donor-acceptor distance to the Förster radius, r/r₀. Use the Autoscale button or the cursors in the parameter histogram to adjust the parameter range, or type the desired range into the Colour Range Min / Max parameters.

Save the data. If you plan to publish the images, export a bmp file.

Contact:

Wolfgang Becker

Becker & Hickl GmbH

Berlin, Germany

Email: becker@becker-hickl.com